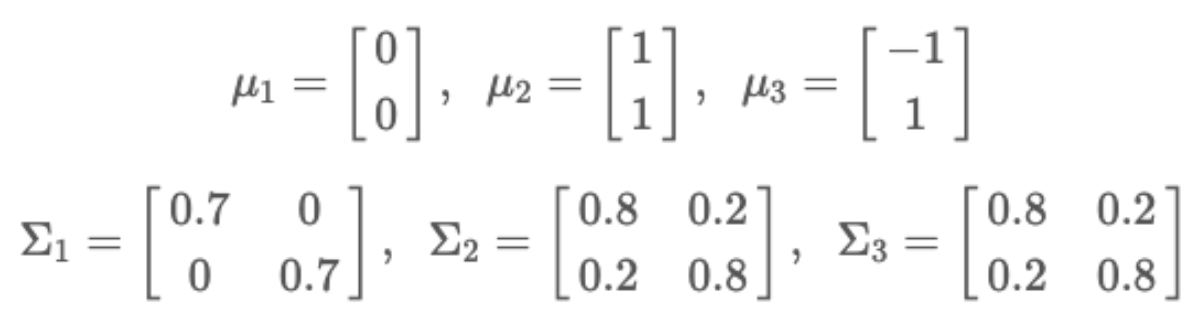Discriminant Analysis

[ML] 선형 판별 분석과 이차 판별 분석

Week#7-1 / Video / Reference: Prof.Choi

회귀나 분류 문제 해결을 위한 다양한 솔루션이 존재한다.

KNN
Logistic Regression
LDA
Bayesian
Decision Tree
SVM
Ensemble
Kmeans
…

하지만 과연 기계학습은 회귀와 분류 문제가 전부일까? 그렇지 않다. 아래 첫 번째 리스트는 AAAI2021, NeurIPS에서 가져온 Research Areas in Machine Learing이고, 그래프는 ICLR 2019 국제 학술대회의 논문들 속 키워드를 분석한 것이다. 수많은 문제, 토픽들이 존재하는 것을 알 수 있다.

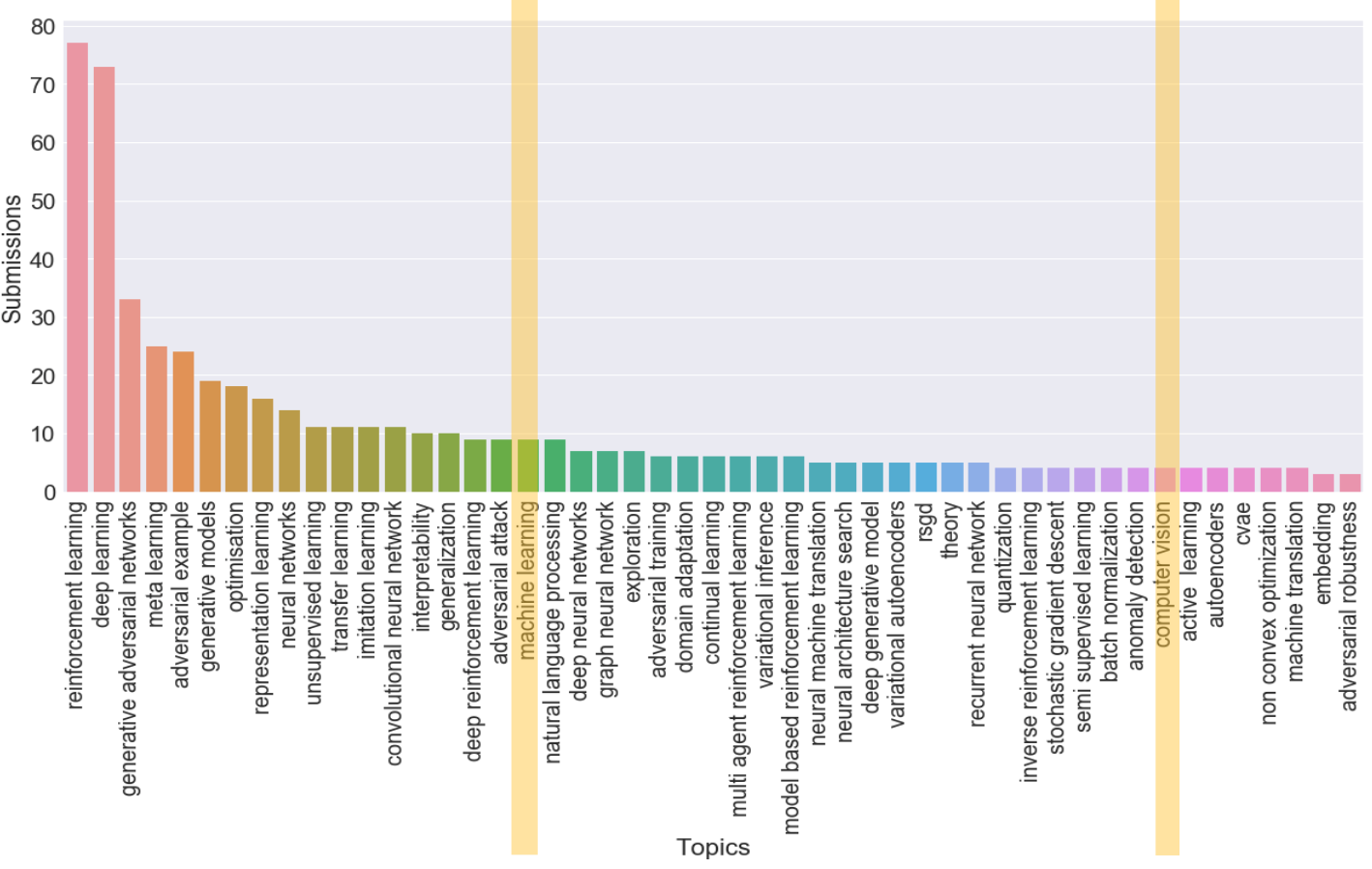
기본기를 탄탄히 다진 후 원하는 분야를 위주로 깊이 탐구해 보는 것이 목표이며, 현재로써는 모든 공부가 기초를 다지는 과정이라 생각한다.

Discriminant Analysis

판별 분석이란 두 개 이상의 모집단에서 추출된 표본들이 지니고 있는 정보를 이용하여 이 표본들이 어느 모집단에서 추출된 것인지를 결정해 줄 수 있는 기준을 찾는 분석법이다. 분류 문제에 사용할 수 있다. 여기서 모집단이라 함은 연구자가 알고 싶어하는 대상(전체 집단)을 뜻하고, 표본은 연구자가 측정, 관찰한 결과의 집합을 뜻한다.

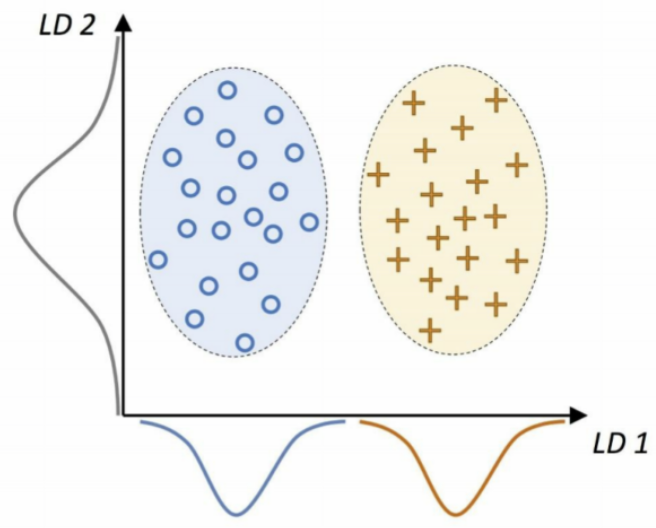
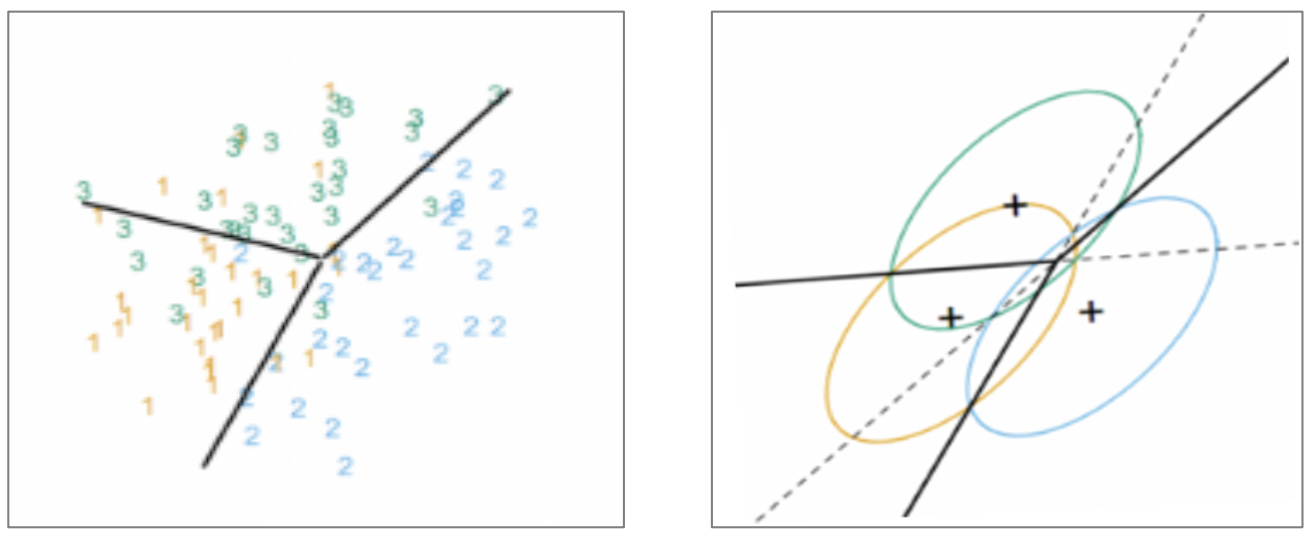
위 그래프에서 두 가지 예시를 볼 수 있다.

좋은 기준: 𝒙₁(LD 1)에 투영된 선형 판별 벡터는 두 가지 class로 잘 구분해 준다.
나쁜 기준: 𝒙₂(LD 2)에 투영된 선형 판별 벡터는 class 판별 정보가 없어 좋은 선형 판별 벡터가 아니다.

정보는 sample로부터 판단한 데이터의 분포, 투영은 각 축에 내린 수선의 발 개념으로 이해하면 된다.

판별 분석을 적절히 사용할 수 있는 예시가 있다.

은행에서 부동산 담보 대출을 행하고자 할 경우 과연 이 채무자가 대출금을 갚을 것인가?

이 경우, 과거 대출금을 반환하지 않은 사람의 정보 유형(연령, 소득, 결혼 유무 등)을 참고하여 담보 신청 시 신청자의 정보 유형을 과거의 유형과 비교함으로써 장래 변제 가능성을 파악할 수 있다. 이는 학습 기반 분류 방법의 핵심 개념이다.

Concepts

Discriminant variable 판별 변수
- 어떤 집단에 속하는지 판별하기 위한 변수로서 독립 변수 중 판별력이 높은 변수를 뜻한다. 이 판별 기여도 외에 고여해야 할 사항은 다른 독립 변수들과의 상관관계이며, 상관관계가 높은 두 독립변수를 선택하는 것보다는 두 독립변수 중 하나를 판별 변수로 선택하고 그것과 상관관계가 적은 독립변수를 선택함으로써 효과적인 판별 함수를 만들 수 있다.
Discriminant function 판별 함수
- 각 개체는 여러 집단 중에서 어느 집단에 속해 있는지 알려져 있어야 하며(supervised learning), 소속 집단이 이미 알려진 경우에 대해 변수들(𝒙)을 측정하고 이들을 이용하여 각 집단을 가장 잘 구분해낼 수 있는 판별식을 만들어 분별하는 과정을 포함한다.
  
  즉, 판별 함수를 이용하여 각 개체들이 소속 집단에 얼마나 잘 판별되는가에 대한 판별력을 측정하고 새로운 대상을 어느 집단으로 분류할 것이냐를 예측하는 데 주요 목적이 있다.
Discriminant score 판별 점수
- 어떤 대상이 어떤 집단에 속하는지 판별하기 위해 그 대상의 판별 변수들의 값을 판별 함수에 대입하여 구한 값을 뜻한다.
Scale 표본의 크기
- 전체 표본의 크기는 통상적으로 독립변수의 개수보다 3배 (최소 2배) 이상 되어야 한다.
- 종속 변수의 집단 각각의 표본 크기 중 최소 크기가 독립변수의 개수보다 커야 한다.
  
  판별력을 좌우하는 것이 전체 표본의 수가 아니라 가장 적은 집단의 표본 수이기 때문이다.

Steps

case가 속한 집단을 구분하는 데 기여할 수 있는 독립 변수 찾기
집단을 구분하는 기준이 되는 독립변수들의 선형 결합, 즉 판별 함수 도출하기
도출된 판별 함수에 의해 (train data) 분류의 정확도 분석하기
판별 함수를 이용하여 새로은 case (test data) 가 속하는 class 예측하기

독립 변수는 Feature engineering, 판별 함수는 다양한 기계학습 방법론을 통해 학습하는 대상이라 보면 된다. 판별 함수의 경우 판별 점수의 집단 간 변동과 집단 내 변동의 배율을 최대화하는 것으로 도출해야 한다.

Background

Assumptions
- 각 class 집단은 normal distribution(정규분포) 형태의 확률 분포를 가진다.
- 각 class 집단은 covariance(비슷한 형태의 공분산) 구조를 가진다.
  
  공분산은 확률변수 2개의 상관 정도를 나타내는 값이다.
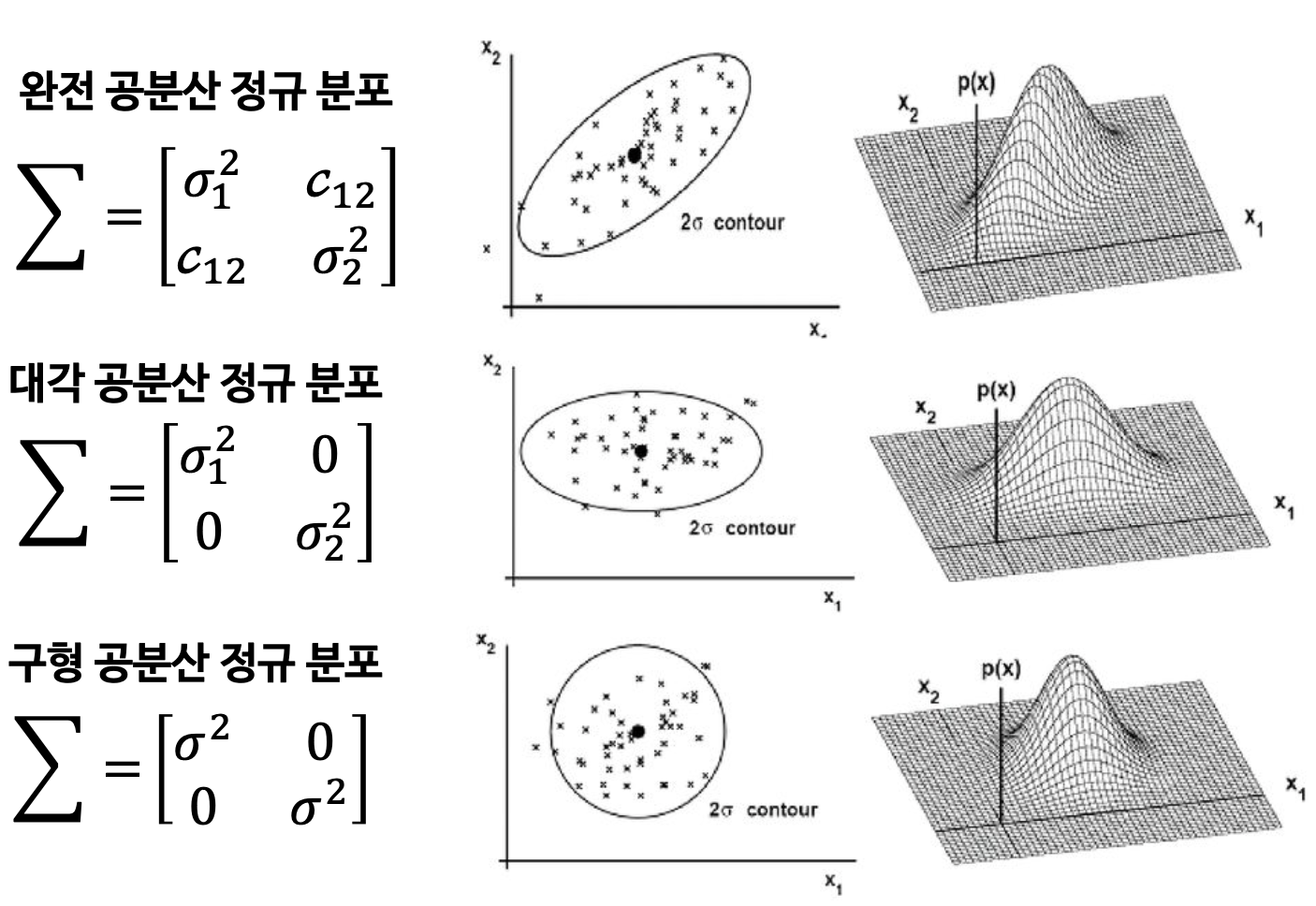
Functions

DA는 판별과 차원 축소의 기능을 한다.
- 2차원의 데이터를 1차원에 projection해서 차원을 축소시킨다.
  
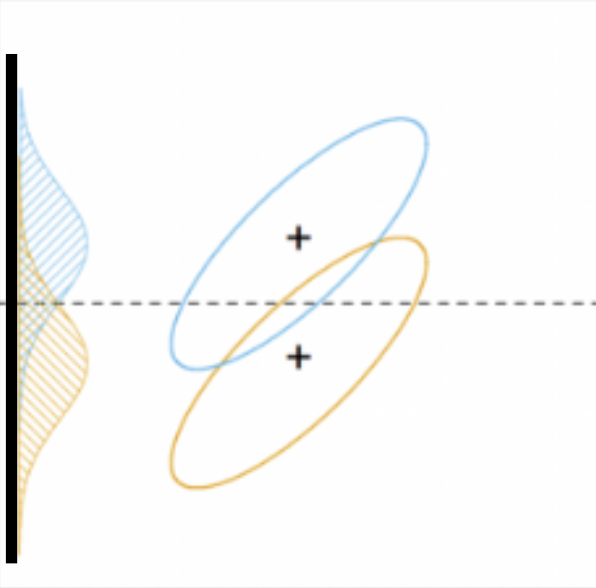
  잘 분리된, 잘 분석되는 녀석들은 굳이 DA를 할 필요가 없다. 데이터가 겹쳐져 있어서 잘 모를 때, 구분하는 축을 찾을 때 DA를 사용한다고 보면 된다.
Decision boundary
- Projection 축(실선)에 직교하는 축(점선)이다.
- 정사영(projection)은 두 분포의 특징이 아래 목표를 달성해야 한다.
  - 평균의 차이가 큰 지점
  - 분산이 작은 지점
  즉, 분산 대비 평균의 차이를 극대화하는 결정 경계를 찾고자 하는 것이다.
  tip. 사영 데이터의 분포에서 겹치는 영역이 작은 결정 경계를 선택하면 된다.
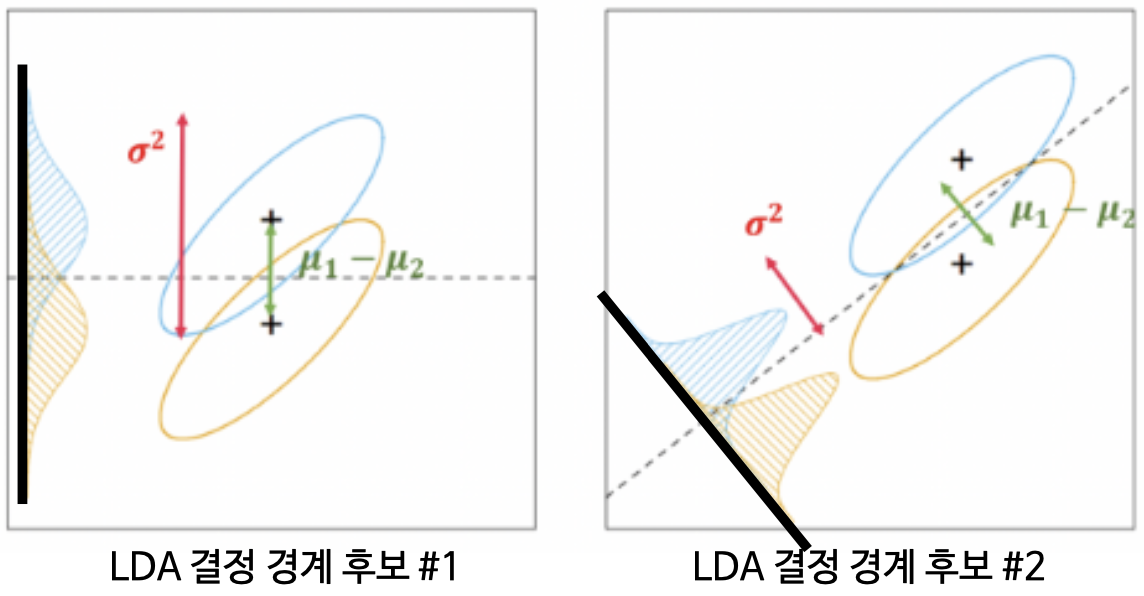
LDA Overall
- 장점
  - 변수(𝒙) 간 공분산 구조를 반영한다.
  - 공분산 구조 가정이 살짝 위반되더라도 비교적 Robust하게 동작한다.
- 단점
  - 가장 작은 group의 sample 수가 설명변수의 개수보다 많아야 한다.
  - 정규분포 가정에 크게 벗어나는 경우 잘 동작하지 못한다.
  - 범주(𝒚) 사이에 공분산 구조가 많이 다른 경우를 반영하지 못한다.
    
    이는 QDA, 이차 판별 분석을 통해 해결 가능하다.

Quadratic Discrimination Analysis

K(범주의 수)와 관계 없이 공통 공분산 구조에 대한 가정을 만족하지 못하면 이차 판별 분석을 적용할 수 있다. 즉, Y의 범주 별로 서로 다른 공분산 구조를 가진 경우에 활용이 가능하다.

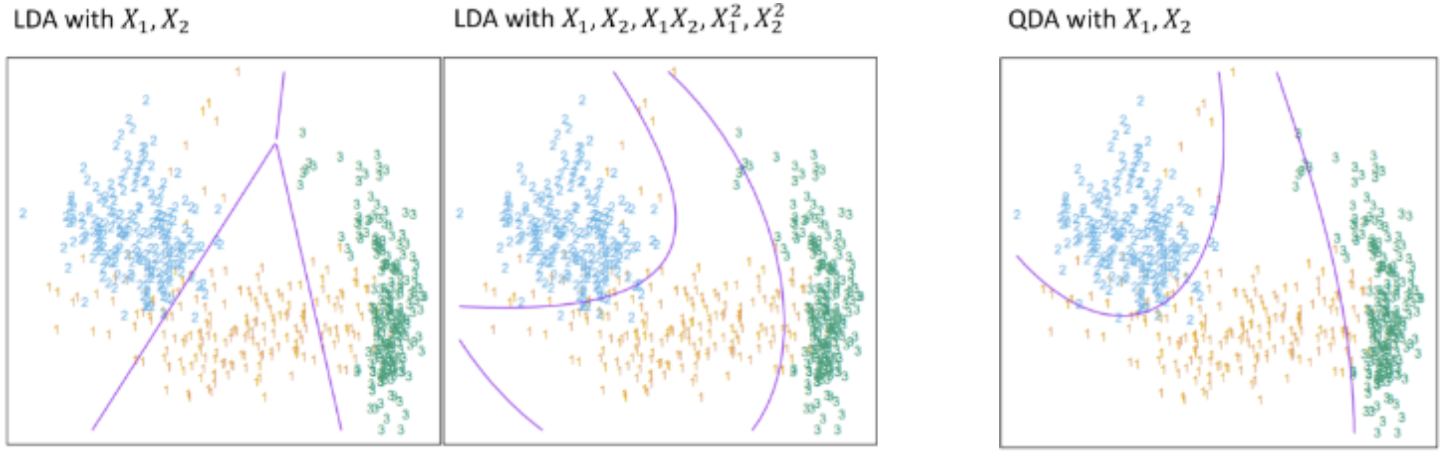
vs LDA

첫 번째 그림을 참고하면 LDA의 결정 경계는 선형으로 가정하고 있어서 서로 다른 공분산 분류에 어려움이 있다.
단, 두 번째 그림을 참고하면 LDA도 같은 공분산의 비선형 분류가 가능하다.

변수의 제곱을 한 추가적인 변수들을 통해 보완하는 방식이다.
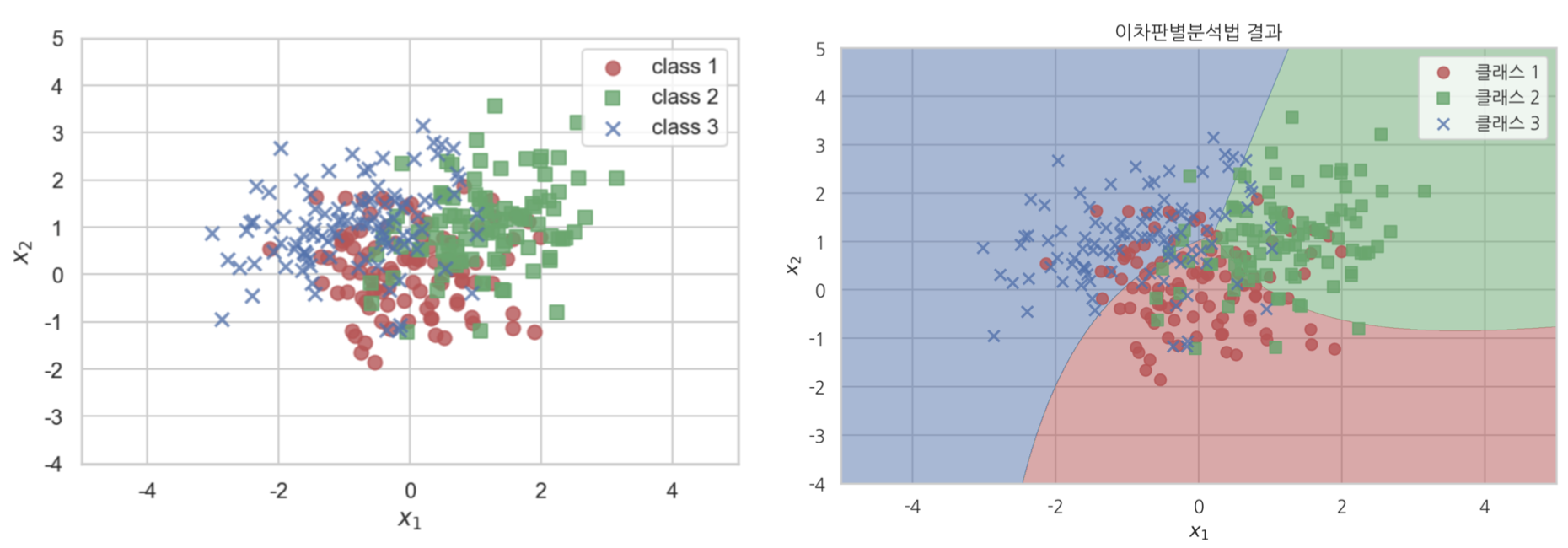
세 번째 그림을 참고하면 QDA는 서로 다른 공분산 데이터를 분류할 수 있다.

비선형 분류가 가능하다는 상대적 장점이 있다.
하지만 QDA는 서로 다른 공분산 데이터 분류를 위해 많은 sample이 필요하다.

이는 설명변수의 개수가 많을 경우 추정해야 하는 모수가 많아지고 연산량이 커진다는 단점으로도 볼 수 있다.

Example

Class 별 서로 다른 모수를 갖는 정규분포를 분석해보겠다.

예를 들어 𝒚가 1,2,3 이라는 3개의 class를 가지고 각 class에서의 𝒙의 확률분포가 다음과 같은 기대값 및 공분산 행렬을 가진다고 가정하자.
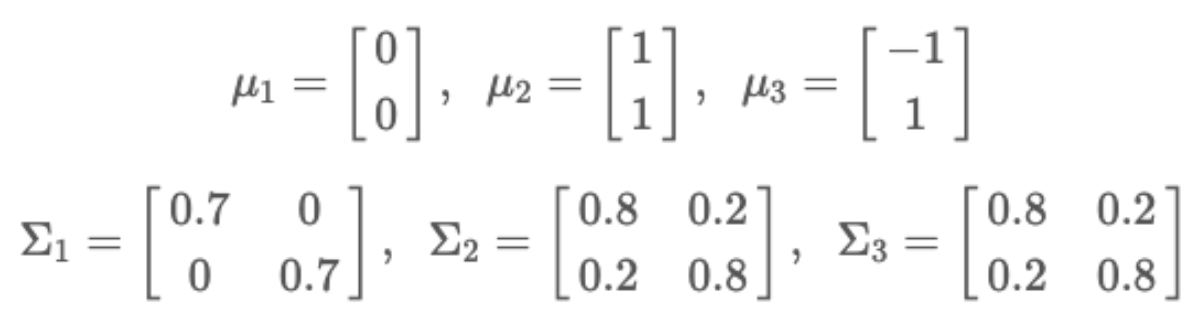
𝒚의 사전 확률은 다음과 같이 동일하다.